Tabular Value-Based Reinforcement Learning

Reading Notes about the book Deep Reinforcement Learning written by Aske Plaat

Recently, I have been reading the book Deep Reinforcement Learning written by Aske Plaat. This book is a good introduction to the theory of Deep Reinforcement Learning. And it is very inspiring when I learn the theory of Deep Reinforcement Learning.

Tabular Value-Based Reinforcement Learning

Tabular Value-Based Agents

Reinforcement learning paradigm: an agent and an environment. The origin of this concept can be traced back to the process that human interacts with the objective world. I ploted a graphical depiction to demonstrate the relationship showed as follows.

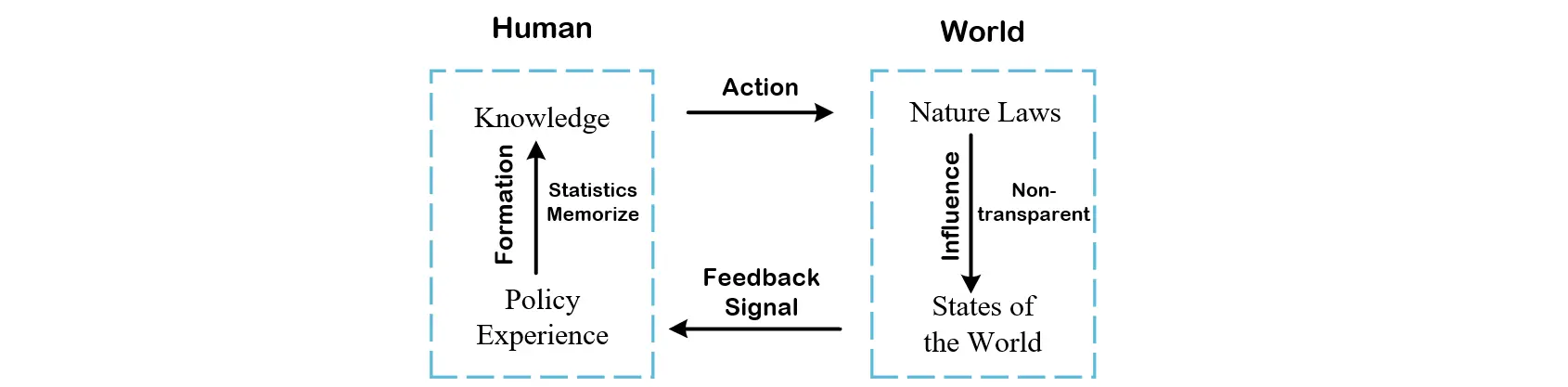
• Agent and Environment
  Formally, we can represent the relationship in the figure above.

  • $S_t\stackrel{a_t}{\longrightarrow} S_{t+1}$
  • $S_{t+1}\stackrel{r_{t+1}}{\longrightarrow} a_{t+1}$

• Features

  • The environment gives us only a number as an indication of the quality of an action;
  • We can generate as many action-reward pairs as we need, without a large hand-labeled dataset (action and reward, action and reward…)

Markov Decision Process

Sequential decision problems can be modelled as Markov decision processes(MDPs).
The Markov property

• the next state depends only on the current state and the actions available in it(no-memory property)

Define a Markov decision process for reinforcement learning as a 5-tuple ($S, A,T_a,R_a,\gamma$)

• $S$ is a finite set of legal states of the environment

• $A$ is a finite set of actions($A_s$ is the finite set of actions in state $s$)

• $T_a(s, s’)=Pr(s_{t+1}=s’|s_t=s, a_t=a)$ is the probability that action $a$ in state $s$ at time $t$ will transition to state $s’$ at time $t+1$

• $R_a(s,s’)$ is the reward received after action $a$ transitions state $s$ to state $s’$

• $\gamma\in[0, 1]$ is the discount factor representing the difference between future and present rewards.

• State $S$

  • State Presentation: the state $s$ contains the information to uniquely represent the configuration of the environment.
  • Deterministic Environment
    In discrete deterministic environments the transition function defines a one-step transition. That is, each action deterministically leads to a single new state.
  • Stochastic Environment
    The outcome of the action is unknown beforehand by the agent because of continuous state space. And that result depends on elements in the environment.
    So we can conclude that the stachastic environment determines the stochastic states.

• Action $A$

  • An action changes the state of the environment irreversibly.
  • Actions that the agent performs are also known as its behavior, just as the human’s behavior.
  • Discrete or Continuous Action Space
    • Action Space is related to the specific application for example, the actions in board games are discrete, while the actions in robotics are continuous.
    • Value-Based methods work well for discrete action spaces, and Policy-Based methods work well for both action spaces.

• Transsition $T_a$

  • Model-Free Reinforcement Learning
    Only the environment has access to the transition function while the agent has not. In this pattern, the transition $T_a(s, s’)$ equals to the nature laws that is internal to the environment, which the agent does not know.
  • Model-Based Reinforcement Learning
    There the agent has its own transition function, an approximation of the environment’s transition function, which is learned from the environment feedback. In my opinion, that is just our policy experince which is summarized from the past feedbacks.

The dynamics of the MDP are modelled by transition function $T_a(\cdot)$ and reward function $R_a(\cdot)$.
In Reinforcement Learning, reward learning is learning by backpropagation. In the dicision tree, action selection moves down, reward learning flows up. To be detailed, the downward selection policy chooses which actions to explore, and the upward propagation of the error signal performs the learning of the policy.

• Reward $R_a$
  Rewards are associated with single states, indicating their quality.
• Value Function $V^\pi(S)$
  Usually, we are most often interested in the quality of a full decision making sequence from root to leaves. So the expected cumulative discounted future reward of a state is called the value function.
• Discount Factor $\gamma$
  In continuous and long running tasks it makes sense to discount rewards from far in the future in order to more strongly value current information at the present time. In my view, it’s just weights factor for every time point.
• Policy $\pi$
  The policy $\pi$ is a conditional probability distribution that for each possible state specifies the probability of each possible action. Formally, the function $\pi$ is a mapping from the state space to a probability distribution over the action space:

$$
\pi: S\rightarrow p(A)
$$

For a particular probability from this distribution we notes: $\pi(a|s)$.
A special case of a policy is a deterministic policy, denoted by $\pi(s)$, and the mapping:

$$
\pi: S\rightarrow A
$$